Bezpieczeństwo w sieci to ukryte algorytmy matematyczne. Zrozumienie działania mechanizmów kryptograficznych jest podstawą tworzenia skutecznych systemów informatycznych. W artykule zaprezentowane zostały informacje o dodatkowych mechanizmach bezpieczeństwa, do których należą: ślepe podpisy, systemy progowe i anonimowe kanały.
Ślepe podpisy
Idea ślepych podpisów została zaprezentowana w 1982 roku przez Davida Chauma. Polega ona na tym, że osoba otrzymująca zaszyfrowany plik podpisuje poprawność dokumentu nie znając jego zawartości. Mechanizm ten można porównać do użycia koperty i kalki. Strona wysyłająca, nazwijmy ją, Alicja wysyła do strony odbierającej, nazwanej Bob, zaklejony w kopercie dokument z informacją oraz kalką. Bob otrzymując kopertę potwierdza jej odbiór popisując się na niej nie otwierając jej. Jego podpis zostaje przez kalkę powielony na zamkniętym dokumencie. Ślepe podpisy mogą być implementowane za pomocą algorytmu RSA. Procedury symetrycznego szyfrowania nie są zwykle używane w czystej postaci, ponieważ w przypadku tych algorytmów zarządzanie kluczami jest zbyt skomplikowane. Dużo lepsze efekty daje stosowanie procedur hybrydowych. Stąd też najczęściej korzysta się z tymczasowych kluczy symetrycznych dołączanych do szyfrowanej nimi wiadomości, a następnie traktuje się je mocnym, asymetrycznym algorytmem RSA.
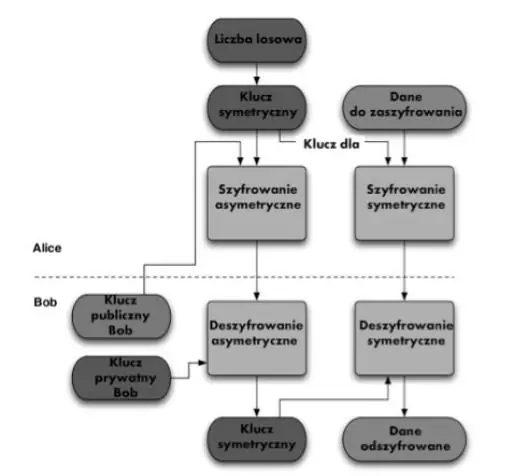
Rys. 1 Procedury mieszane z wykorzystaniem algorytmu RSA
Alicja koduje wiadomość przed jej przesłaniem używając czynnika generowanego na podstawie klucza publicznego Boba. Alicja losuje liczbę r, która jest liczbą pierwszą. Następnie obliczana jest zakodowana wiadomość m. Bob otrzymuje zakodowaną wiadomość i do rozkodowania potrzebuje cząstkę wykładniczą. Wiadomość m wysyłana zostaje do Alicji która używając odwrotności r eliminuje z wiadomości r i otrzymuje wiadomość m podpisaną przez Boba.
2. Systemy progowe
Załóżmy istnienie pewnego sekretu S. Sekret taki można przesłać w całości ale jest on narażany na rozszyfrowanie. Istnieją sprawdzone metody, którą pozwalają dobrze zabezpieczyć informację. Należą do nich systemy progowe dzielące sekret w taki sposób, że do odtworzenia potrzebna jest pewna ilość jego części. Istnieje pewna para liczb na które podzielono sekret a m oznacza minimalną ilość części potrzebnych do odtworzenia sekretu. Przykładami systemów progowych są zaprezentowane niezależnie w 1979 roku protokoły: Blakley’a oraz Shamira. Oba te protokoły mają dwa istotne ograniczenia:
- Każdy fragment sekretu musi mieć długość co najmniej równą długości sekretu
- Protokół musi używać losowych bitów
Jeżeli przyjmiemy, że sekret S jest pewną liczbą z przedziału od 0 do n-1 to losujemy dla każdego uczestnika oprócz ostatniego liczbę S i z tego samego przedziału. Wszyscy uczestnicy za wyjątkiem ostatniego nie znają sekretu, ponieważ otrzymali losowe liczby Si . Jeśli będzie brakowało jakiegoś innego, k-tego, uczestnika, to pozostali będą mogli dodając swoje kawałki otrzymać liczbę S − SK . Tylko k-ty uczestnik zna liczbę SK. Rozważmy przykład: Sekret S jest liczbą z przedziału od 0 do 999 i S=803. Rozpatrzmy trzech uczestników, z których pierwszy losuje liczbę S1=272 a drugi liczbę S2 =995. Więc:
S3 = 803 − 272 − 995mod 1000 = − 464mod 1000 = 1000 − 464 = 536
Aby wszyscy uczestnicy mogli poznać sekret dodają swoje fragmenty otrzymując:
S=S1 + S2 + S3 mod 1000 = 1803mod 1000 = 803
Protokół Blakley’a jest przykładem systemu progowego gdzie do odtworzenia klucza wymagane są wszystkie jego części. Opiera się na założeniu, że do wyznaczenia punktu w n-wymiarowej przestrzeni potrzeba n podprzestrzeni o wymiarze n-1.
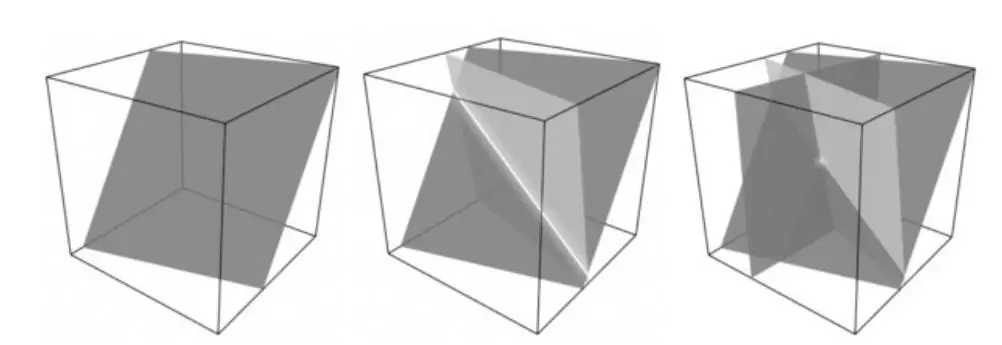
Rys.2 Protokół Blakley’a dla trzech wymiarów
3. Anonimowe kanały
Chcąc ukryć tożsamość nadawcy można użyć mechanizmu anonimowego kanału uniemożliwiającego ukrycie tożsamości nadawcy. Mechanizm ten opiera się na sieciach mieszających składających się z serwerów Proxy, z których każdy posiada swój klucz publiczny i prywatny. Wiadomość przesyłana przez sieć mieszającą musi być zaszyfrowana kluczem publicznym serwera, który jako ostatni przesyłał wiadomość. Do przesłania potrzebna jest losowa wartość Nonce dodawana w celu uniemożliwienia odczytania funkcji mieszającej serwera. Wiadomość m gotowa do wysłania przez sieć mieszająca może być opisana jako:
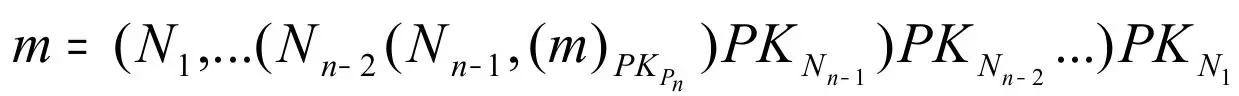gdzie:
n – ilość serwerów mieszających
Ni – i-ta wartość Nounce
PKi – klucz publiczny i-tego serwera
Każdy serwer po otrzymaniu wiadomości odszyfrowuje ją redukując wartość Nounce. Następnie wiadomość zostaje przemieszana za pomocą funkcji mieszającej i zostaje przesłana do kolejnego serwera. Dopiero ostatni serwer po rozszyfrowaniu uzyskuje rozkodowaną wiadomość m.
4. Podsumowanie:
Tradycyjne metody przesyłania wiadomości ulegają zmianom. Wraz z rozwojem technologii informacyjnych coraz więcej poufnych danych przesyłanych jest drogą elektroniczną. Stąd nacisk na zapewnienie bezpieczeństwa przesyłanym wiadomościom. Wykorzystując ślepe podpisy, systemy progowe i anonimowe kanały tworzymy mechanizmy do skutecznego zabezpieczenia krążących w sieci danych. Wymienione metody stanowią stale rozwijającą się, potężną dziedzinę wiedzy, która wymaga tworzenie coraz to nowych rozwiązań.
